Cares aristas i vèrtexs (1a part)

Geometric solids

Un applet per comptar cares, arestes i vèrtexs i verificar la relació d'Euler.


En la posició "solid" permet observar el cos, acolorir-lo, moure'l, fer-lo transparent, etc. En la posició "net" apareix el desevolupament.

Per què aquest applet?

En posició "sòlid" el problema de comptar cares, arestes i vèrtexs es facilita gràcies a que els cossos es poden fer transparents i es pot moure la figura. De totes maneres, com que no aporta molt a la manipulació del poliedre en 3D, pot jugar el paper de simulador en cas de no disposar d'una col·lecció de cossos prou ampli per poder fer-ho.

En posició "net", comptar sobre el desenvolupament, és una activitat molt interessant ja que és fàcil comptar les cares però comptar arestes i vèrtexs implica tenir en compre com es plega el poliedre.

Comentaris

Juan Garcia Moreno proposa un altre applet amb la mateixa finalitat

Del mateix autor, un altre applet difícil però molt maco, que pensem que pot servir perquè us trenqueu el cap els docents i després trieu quins cal plantejar a alumnes als que els agradin els reptes.

I per finalitzar un vídeo-qüestionari sobre el tema

També trobareu qüestionaris d'aquest tipus als diferents nivells de Faces, Edges and Vertices

Joc de detectius: seguint el residu

The remainders game
Un "joc de detectius" en el món de l'ensenyament de les Matemàtiques és aquell en el que es presenta el repte d'endevinar un objecte matemàtic "amagat" a partir de pistes, que porta als alumnes a fer un treball sistemàtic de "filtre" per trobar l'objecte buscat.  

Exemples de propostes de jocs de detectius per als més petits
(Cerezo, A., Calvo, C. & Barba, D., 2013, El bloc de MATES. Editorial Barcanova) 

The remainders game és un fantàstic applet que gira la truita: el nombre secret està entre 0 i 100 però en aquest cas és l'usuari el que ha de triar. entre una oferta amplia, quines pistes vol utilitzar. Totes les pistes són del mateix estil: dóna el residu de la divisió del nombre secret entre 2, 3, 4, 5, 6, 7, 8 o 9. Cal triar-ne una, veure que passa després una altra etc. El repte està en fer-ho en el mínim d'intents possible. Com menys pistes s'utilitzin més punts s'obtenen.

Preguntes clau

• Per quin nombre començaries a preguntar? (per exemple si comencem pel 6 traiem la mateixa informació que fent primer el 2 i després el 3?) 
• Per quina raó has proposat dividir per "n" en el pas ...
• Un company teu està en aquest moment del joc (veure imatge superior)  Pot saber el nombre? i si no quin pas faries posteriorment, perquè?

Comentaris

• Segons l'edat dels alumnes podem donar una graella del 100  per facilitar la tasca d'anar marcant els nombres que anem eliminant, Encara que si volem crear hàbits de treball hem de gestionar que se'n surtin utilitzant un paper en blanc.
• Des del punt de vista de la comunicació i la justificació del procés recomanaríem fer-los fer un informe d'una de les "partides" on expliqués els passos fets i es plantegi si hi havia un camí més curt

Joc de divisors

Factor Game

Joc de divisors (on convé saber trobar tots els divisors). En la seva primera versió, el tauler era fix i de l'1 al 30 que és una bona mida per fer el joc interessant. La seva última actualització permet triar la mida del tauler de joc, el que permet començar per taulers petits per anar familiaritzar-se amb les primeres estratègies

El primer jugador tria un nombre i guanya tants punts com el nombre que ha triat. i el segon jugador ha d'escriure tots els seus divisors i guanya tats punts com la seva suma. Si se'n deixa algun la màquina l'informa. Després es canvien les tornes. A mesura que els nombres són utilitzats queden marcats sobre el tauler i ja no es poden utilitzar més. Guanya qui suma més punts

 

Per què aquest applet?

• Per exercitar el càlcul de divisors d'un nombre, i motivar a buscar una estratègia de recerca que faci que no se'n deixin cap.
• Per aplicar les propietats dels nombres a l'estratègia a utilitzar per jugar: què es millor jugar un nombre primer, un de quadrat? en quin moment
• Per a parlar i utilitzar nombres abundants: la suma dels seus divisors propis és més petita que el nombre, deficients: la suma de divisors és inferior, o perfectes: la suma és la mateixa.

Informació al Puntmat

Tant a divisors i pensament exhaustiu, com a applets de divisibiltat, hi trobareu més informació sobre aquest applets i altres activitats relacionades amb el tema.

Preguntes clau

• Per quin nombre has de començar la partida, perquè?
• (en un moment de la partida) fer una foto de pantalla i justificar el nombre que has triat 
• Com ens ho podem fer per no deixar-se cap divisor?. Segurament dir els divisors "per parells" o "mirall" el 2 amb el 24 el 3 amb el 16 ... (en el cas del 48)

Informació complementària
Un altre applet amb un joc semblant a l'anterior pero més difícil

En l'applet següent s'han de tatxar tots els divisors del nombre indicat (53) o del resultant de canviar l'ordre de les seves xifres (35) cal triar quin és més interessant per a tu, tenint en compte que guanyaràs tants punts com la suma dels divisors tatxats. Per tant, en cada jugada l'estratègia òptima és enumerar tots els divisors dels dos nombres possibles i avaluar la seva suma. Val a dir que quan oblides tatxar algun divisor l'applet et renya!

buscar un número

Largest Even i Dozen
Són dos applets de la pàgina de l'nrich que responen a la filosofia de la pràctica productiva. El primer treballa aspectes de paritat (parells - senars) i el segon criteris de divisibilitat.

Largest Even

Un applet per ser portat a classes de cicle inicial o mitjà, i es tracta d'aconseguir el nombre més alt de dues xifres. El presentem a partir d'una seqüencia realitzada per un alumne.

• Es pot triar parell o senar, un cop triat "New dígit" genera un nombre d'una xifra. En el cas de la imatge  ha estat el 5
• L'usuari ha triat el 9 per construir el 95, que si bé és un nombre alt no és parell

http://nrich.maths.org/7431

L'usuari rectifica i canvia l'orde posant el 59, que tampoc és parell

Finalment troba la solució demanada

 Per què aquest applet?

• És una molt bona activitat de pràctica productiva ja que el seu objectiu és trobar el nombre més gran, però s'està treballant paral·lelament la idea de parell i senar
• Es pot anar més enllà plantejant que donin instruccions a un robot perquè resolgui de manera correcte aquest tipus de situacions: La tercera pregunta clau planteja el que volem dir

Preguntes clau

• Si el nombre es que genera es parell i has d'aconseguir el parell més gran quin nombre entraries? què faries després, com els ordenaries?
• I en cas que el nombre que genera sigui senar?
• Sabries escriure les instruccions perquè un robot pogués sortir-se'n sempre ?

Dozens
Amb la mateixa idea trobem un altre applet per a cicle superior de Primària i ESO, en aquest cas el que es treballa es divisibilitat

 http://nrich.maths.org/559

• Triar el nombre sobre el que buscar els seus múltiples, les opcions són 2,3,4 i 6.
• Després l'applet genera dues xifres 
• Cal trobar el nombre de tres xifres més gran possible que sigui múltiple del triat.

Comentaris
Un cop conegut el joc, podem proposar una activitat: jugar un altre cop i demanar que redactin el procés que han seguit per a triar el nombre. Amb el 4 i el 6 les situacions que es creen poden ser interessants.
Per exemple podríem plantejar la situació col·lectivament en pantalla,  que els alumnes treballant per grups ho resolguin i finalment comprovar les diferents propostes en pantalla de manera col·lectiva

Tot i així es perd la interactivitat i és un treball "dinàmicament" completament diferent al que es produeix quan es fa amb l'applet. Depen del vostre objectiu triareu una opció o l'altre.

Transvasament de líquids

A continuació hi ha tres applets relacionats amb el famós problema de com mesurar una quantitat entera de litres d'aigua quan només es disposen de dos recipients de capacitat coneguda (per exemple, 5 i 9L)   

http://nlvm.usu.edu/en/nav/frames_asid_273_g_2_t_4.html 

http://pbskids.org/cyberchase/games/hardproblems/ 

http://www.transum.org/Software/Investigations/jugs.asp
(a la part inferior es pot variar la capacitat de les gerres)

http://www.mathsatplantsbrook.co.uk/Primary/Puzzles/qtn_jugs.swf

Comentaris:

• Al blog del Joan Jareño hi ha una fantàstica entrada (amb animacions interactives) relacionada amb aquest mateix problema: Problemes de garrafes 
• A la pel·lícula "Difícil de matar: La venjança" protagonitzada per Bruce Willis (1995) apareix aquest joc amb recipients disponibles de 3 i 5 galons amb els que el protagonista ha d'obtenir 4 galons. I, sobre tot, val la pena mirar la paròdia que en fan Cruz y Raya.
• Platejat el problema a alumnes de Cicle Superior de Primària va resultar molt interessant la discussió de bones maneres de representar les etapes seguides per arribar a la solució. En aquest cas ho vam fer en format còmic, encara que val a dir que no els va ser fàcil d'entrada, els va costar bastant.
• Es pot aprofundir sobre aquest problema a  Jug Problem, Water-Pouring Problem o The Three Jugs Problem  

Factors Line

Es tracta d'un applet per practicar múltiples i divisors que demana les diferents possibilitats de col·locar alguns nombres (en el cas de la imatge 1,2,3 i 21) sobre cel·les diferents de la graella de manera que:

• cada nombre va sobre un cel·la que té un múltiple o un divisor del nombre
• les cel·les estan alineades i sense espais entre elles en horitzontal, vertical o diagonal

http://nrich.maths.org/1138

 El botó d'edició permet modificar:

•  la quantitat de nombres que s’han de posar en línia (Line length). Per exemple: 
• quan es tria 4: les línies han de ser de 4 elements: un múltiple d’1, un múltiple o divisor de 2, un múltiple o divisor de 3 i un múltiple o divisor de 21    
• quan es tria 5: les línies han de ser de 4 elements: dos múltiples  d’1, un múltiple o divisor de 2, un múltiple o divisor de 3 i un múltiple o divisor de 21  
• la mida de la graella ja que el nombre de files i columnes poden variar des de 3 a 12 (Rows & Columns)

El gran problema amagat sota aquest joc és esbrinar quantes solucions diferents hi ha. A l’apartat de solucions de la pàgina del Nrich es troba un estudi de les solucions possibles quan es treballa amb la graella de 5 files i 5 columnes.

Aquí es veu una solució i dues línies vermelles que representen dues solucions trobades anteriorment 

Val la pena destacar que l'applet compta com a diferents dos solucions que utilitzen les mateixes cel·les però cobertes per diferents nombres. Per exemple: una solució és col·locar  l’1 al 4, el 2 al 2, el 3 al 3 i el 21 a l’1  i una altra diferent  l’1 al 4, el 2 al 2, el 3 a l'1 i el 21 al 3. 

Geoplans

Geoplà "beluga"
El Geoplà és un dels materials més famosos en el món de les Matemàtiques. No és d'estranyar trobar a la xarxa forces versions de simuladors d'aquest material.
Començarem per l'últim que hem conegut, i al nostre entendre el que presenta més possibilitats. Per nosaltres és excel·lent. Quan l'obriu recordeu que per començar cal clicar a l'últim botó (rodó) de l'esquerra.

NOTA: a 5/10/2014 l'enllaç no funciona però la pàgina que el conté si. No sabem si tornaran a connectar-ho en breu. Si algú troba l'enllaç demanem que ens ho notifiqui

Per què aquest material?
El geoplà és un dels materials històrics per excel·lencia, conjuntament amb els reglets. Disposar de simuladors per a facilitar les discussions col·lectives, saber mesures automàticament, acolorir per distingir etc amplia les seves possibilitats

Informació al Puntmat
Podeu trobar activitats que utilitzen aquest material en les següents activitats
Geoplans i pensament exhaustiu
Joc del Geoplà: definicions i propietats
Geoplà tangram i mesura de superfície
A la web de l'Espai Jordi Esteve podeu trobar més informació a la fitxa dedicada a Geoplà


Altres simuladors de Geoplà
Us presentem una mostra d'applets de Geoplans. Segurament els més coneguts deuen ser els de la nlvm i (1r,2n,4t i 5è). però n'hi ha d'altres que aporten aspectes interessants amb  diferent presentació i tipus (malla quadrada, isomètrics, circulars)

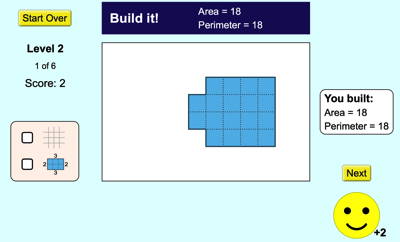
Geoplà estàndard malla quadrada el publicat per la NLVM. Cal dir que no solament permet fer figures i acolorir-les, sinó que a més permet visualitzar les mesures tant d'àrea com de perímetre dels polígons construïts

També proposa activitats

Geoplà que indica coordenades
També de nlvm

Geoplà de Pavel Safronof

Estèticament atractiu. Molts punts i "amable" de fer anar. A més permet fer polígons convexos amb facilitat, cosa que en algunes altres propostes de vegades es fa complicat. 

 (Applet designed and coded by Pavel Safronov. Geoboard animation created by Linda Stojanovska. Contact Pavel Safronov at MSTE offices: 505 East Green Street, Suite 102, Champaign, IL 61820. Information about the Geoboard)

Geoplà isomètric (de la pàgina nlvm) A més de permetre realitzar triangles equilàters, és útil per fer perspectives isomètriques de  figures com cubs i prismes rectangulars. De totes maneres, per fer representacions, l'applet  d'illuminations és molt més directe, tot i que fa alguna cosa imprevista.

Geoplà circular (de la pàgina nlvm) Val la pena complementar aquest material amb l'activitat  Triangles All Around

Catàleg de Geoplans (de la pàgina nrich) Es poden generar geoplans de diferent classe i nombre de punts.

Versió de  Pep Bujosa (que a més assigna coordenades) feta amb Geogebra

Geoplà de Count me in Too. Té l'avantatge que es poden posar en pantalla "col·leccions" de geoplans cosa que permet fer activitats com, per exemple, buscar tots els quadrilàters possibles que es puguin fer en un geoplà de 9 puntes tenir-los tots a la vista.

Math Learning Center. Té un app per a l'Ipad que va molt bé

Geoplano Inteligente (del Juan Garcia Moreno) Proposa uns reptes, que realment ho són.

Joc de productes

Applet per a dos jugadors (o contra la màquina) en el que cal fer quatre en ratlla. Treballa les taules de multiplicar de manera inversa. Donat un nombre ha de buscar dos factors, i marcar-los a la línia inferior. Una fitxa del color del jugador taparà el nombre del tauler si ho ha fet bé, o un altre si ho ha fet malament.

1. El primer jugador tria dos nombres de la barra inferior movent els cursors i el seu producte s'il·lumina a la pantalla 
2. El segon jugador solament pot moure un dels dos nombres de la barra per definir el seu nombre. Aquesta  característics aporta un component estratègic interessant.

Permet canviar les condicions de joc, tant els factors implicats, com la quantitat de nombres que cal posar en línia per guanyar.

L'applet al bloc del Puntmat

• Podeu trobar informació més detallada en el post applets de divisibilitat, conjuntament amb d'altres applets del tema
• També a divisors i pensament exhaustiu bàsicament enfocat  dedicat a divisibilitat

Per què aquest applet?
A cicle mitjà repassar les taules de multiplicar partint del resultat
A cicle superior exercitar la descomposició en factors de nombres (canviant els valors inicials de la barra inferior, l'applet ho permet) ) 

Preguntes clau
Analitzar situacions concertes de la partida per anar descobrint estratàgies eficients, per exemple: veient la situació en aquest moment:

1. Quins serien el millors nombres a triar en una situació determinada?
2. Quin paper juguen els nombres que tenen més d'una resposta, per exemple el 36 (9x4 i 6x6)? Triar-lo té avantatges, o al contrari?
3. Quines estratègies  utilitzes per a guanyar? és a dir. com li pots fer "la punyeta" al contrari? (una d'important és, en el cas que estigui en situació guanyadora, no deixar-li cap factor del nombre que li falta per acabar

Comentaris

• Tot i ser un applet es pot convertir fàcilment en un joc de taula manipulatiu: la figura de l'esquerra és la imatge d'una materialització feta pels alumnes de magisteri musical a l'assignatura de didàctica de les matemàtiques a la UAB. Les boles de la línia inferior serveixen per a indicar el producte triat, en aquest cas 4x8,  fent-les lliscar pel cordill.

• S'aconsella jugar entre parelles, ja que preveure les possibilitats de l'altre i organitzar la teva es complex.
• L'enllaç al joc ofereix informació exhaustiva sobre les possibilitats i posada en pràctica d'aquest applet

Configuració d'entrades Etiquetes divisibilitat, illuminations, jocs, materialitzacions, primària c.mitjà, primària c.superior Publicat a 27/11/13 16:26 Central European Time Enllaç permanent Ubicació Opcions Envia la teva opinió

De quantes maneres puc pagar? (divisibilitat)

Una activitat ja clàssica, o passada de moda, amb l'aparició del correu electrònic,  és la de franquejar una carta amb els segells necessaris per a obtenir l'import necessari, tenint en compte que hi ha segells de diferents preus.

Transum ens regala una calculadora virtual associada a aquest problema en la versió en que demana amb quants segells de 3p  i de 8p es pot  franquejar una carta que val 73p

http://www.transum.org/software/SW/Starter_of_the_day/starter_July8.asp

Després planteja l'activitat, en la que cal arrossegar els segells a cadascuna de les cartes. Com es veu a la imatge la de 33p l'han aconseguit pensant que són tres cops 3+8 (o, onze cops 3). Per aconseguir 52, hauran de trobar quina suma d'un múltiple de 8 i un múltiple de 3 dóna 52, etc

http://www.transum.org/software/SW/Starter_of_the_day/Stamps/Default.asp

Aquesta activitat és "filla" de la plantejada al magnífic llibret d'activitats "Investigando las Matemáticas (2)" de R. Fisher i A. Vince (original del 1988 i traducció del 1990), actualment descatalogat.

Altres propostes relacionades

En el post Matemàtiques anant per carrer (1) del blog del PuntMat, es presenten activitats semblants a aquesta, algunes d'elles incorporen també  applets

Comentari final

En el post, "de quantes maneres puc pagar (descomposicions)" es tracta el mateix problema des d'una perspectiva molt allunyada de la divisibilitat, degut a que un dels "segells" té valor 1, per tant es pot aconseguir qualsevol nombre.

Identificació de nombres primers

Relacionat amb el post Els primers nombres primers presentem aquí alguns applets que col·laboren en la identificació d'aquests nombres.

Un puzle per organitzar els 100 primers nombres primers:

http://www.transum.org/Maths/Activity/Jigsaw/Numbers.asp?Level=10 

Un laberint que podem recòrrer només passant de nombre primer en nombre primer:

http://www.transum.org/Software/Puzzles/Prime_Labyrinth.asp

Un problema relacionat amb la conjectura Goldbach que estableix la possibilitat d'escriure tot nombre parell com a suma de dos nombres primers:

http://nautilus.fis.uc.pt/mn/goldbach/index.html

La conjectura de Goldbach apareix a "La habitación de Fermat"

 

Mesura de superfície: concepte

La Marta Presegué Mestra de l'escola La Sínia de Vic ens ha fet conèixer aquest applet que va treballar a classe amb els seus alumnes de sisè de primària. Les seves eines permeten, desplaçar, girar, i retallar una figura argumentant, si les figures són iguals o si una és més petita o més gran que l'altra.

http://www.fisme.science.uu.nl/toepassingen/00502/  

Per què aquest applet?

Per introduir la mesura de longitud a infantil o cicle inicial, hi ha moltíssimes experiències de comparar i ordenar objectes de la vida quotidiana per poder dir quin és él més llarg, paraula clau sota la que "s'amaga" el concepte de longitud

Aquest treball sobre  el concepte es desdibuixa quan arribem a la mesura de superfície on es prioritza massa ràpidament el pas a les unitats i a les fórmules de càlcul. Aquest applet ens ofereix una proposta fantàstica que treballa precisament aquest aspecte una mica oblidat.

Saber quina de dues figures "és més gran" (paraula clau que amaga "superfície") implica també començar comparant, és a dir retallar la primera per veure si pot tapar completament la segona ens acosta al concepte de mesura de superfície.

Comentaris

1. Com molts dels applets del Freudenthal no es tracta d'una sola activitat, sinó d'una sèrie, en concret 10 en la que el nivell de dificultat va canviant. 
2. Us pot interessar saber que  "oppervlakte rood" = superfície vermella, "oppervlakte grijs" = superfície grisa, "is groter dan" = és més gran que, "is kleiner dan" = és mes petit que i "is even groot als" = és tan gran com.
3. No es casualitat que hi hagi una quadrícula  al darrera. Dóna guies per a facilitar comparacions entre figures retallades i espais lliures recolzant-se en la quadrícula. Per exemple: en la figura inferior es veu clarament que el triangle gris i la punta de sota són la mateixa figura. (base 2 altura 1, per exemple)  De totes maneres si no desplaça el triangle a la part de dalt, i es completa la construcció l'applet no la dona com a bona
4. La quadrícula és una gran eina per ajudar als alumnes a justificar (si els hi demanam) si dues figures són iguals, abans de provar--ho.
   
   

Exemple  d'una seqüència

Situació de sortida

superposar

retallar (apareix un punt blau quan es col·loca el cursor en el lloc de tall)

recol·locar i validar si és més gran, petita o igual que la vermella

l'applet acoloreix l'exercici ben realitzat.

Cal destacar que un cop acabat un exercici, en passar a un altre, el primer guarda la solució, el que permet poder fer una revisió general quan acabin, una copia de pantalla de cadascun etc.

Si hi jugueu uns estona i us agrada segur que el porteu a classe... si teniu infraestructura per fer-ho.

Altres applets per introduir el treball amb càlcul d'àrees:

http://www.mathspad.co.uk/teach/linkedDocuments/areaSquaresHolder.php 

https://phet.colorado.edu/sims/html/area-builder/latest/area-builder_en.html
(funciona amb IPad)